SICPJS 1. Building Abstractions With Functions
Vocabulary
- computational processes(a sorcerer’s idea of a spirit): ideas, can’t be seen or touch but solve the problem and direct the real world
- program(a sorcerer’s spells):prescribe computational processes by programming language, manipulate another abstract thing data.
- programmers(the sorcerer’s apprentice): the one who form an idea and conjure with spells.
- data:
- javascript: our spells format, it inherited its core features from the Scheme, core feature: first-class functions and dynamic typing.
Questions
- How to make your spells do exactly what you want it to do?
- how to vistualize systems in advance(testing?)
- make sure won’t lead to catastrophic consequences when unanticipated problems happen(fault-tolerance?)
- debug the problems when they arise(monitor?)
Notes
- make your spells do exactly what you want it to do
- well designed programs design in modular manner, so that the parts can be constructed, replaced, and debugged separately(human’s limitation, make it simple and stupid! complex ideas are made by several simple ideas, so just break it down.)
1.1 The Elements of Programming
Vocabulary
- primitive expressions, which represent the simplest entities the language is concerned with,
- means of combination, by which compound elements are built from simpler ones, and
- means of abstraction, by which compound elements can be named and manipulated as units.
- data: the stuff we what to manipulate
- function: descriptions of rules to manipulate data
Questions
Notes
- Powerful language server as a framework to organize our ideas about the processes.(pay attention to what language prodive for combine simple ideas. object-orient programming? not only language, framework like react, they provide well design abstraction(virtual dom), and a easy way for organize module frontend component)
1.1.1 Expressions
Vocabulary
- expression: consists of an expression followed by a semicolon.(In my option, a line is basically an expression)
- primitive expression:
- number
- combination expressions:
- an expression composes by others expression(operator combination)
- primitive expression:
Questions
Notes
1.1.2 Naming and the Environment
Vocabulary
- naming: provide for names-value storage, is a simplest mean of abstraction, provide a easy way to reuse the complex value(combination expression)
- environment: the cost of naming(make an value and reuse them after by refer their name) is we must maintain a sort of memory that keep the key-value pairs, this called environment
Questions
Notes
1.1.3 Evaluating Operator Combinations
Vocabulary
Questions
Notes
- we don’t operate the combination expression but the primitive expression like data or a name all the time
- evaluating operatoor combinations is a recursive process in nature, as follow:

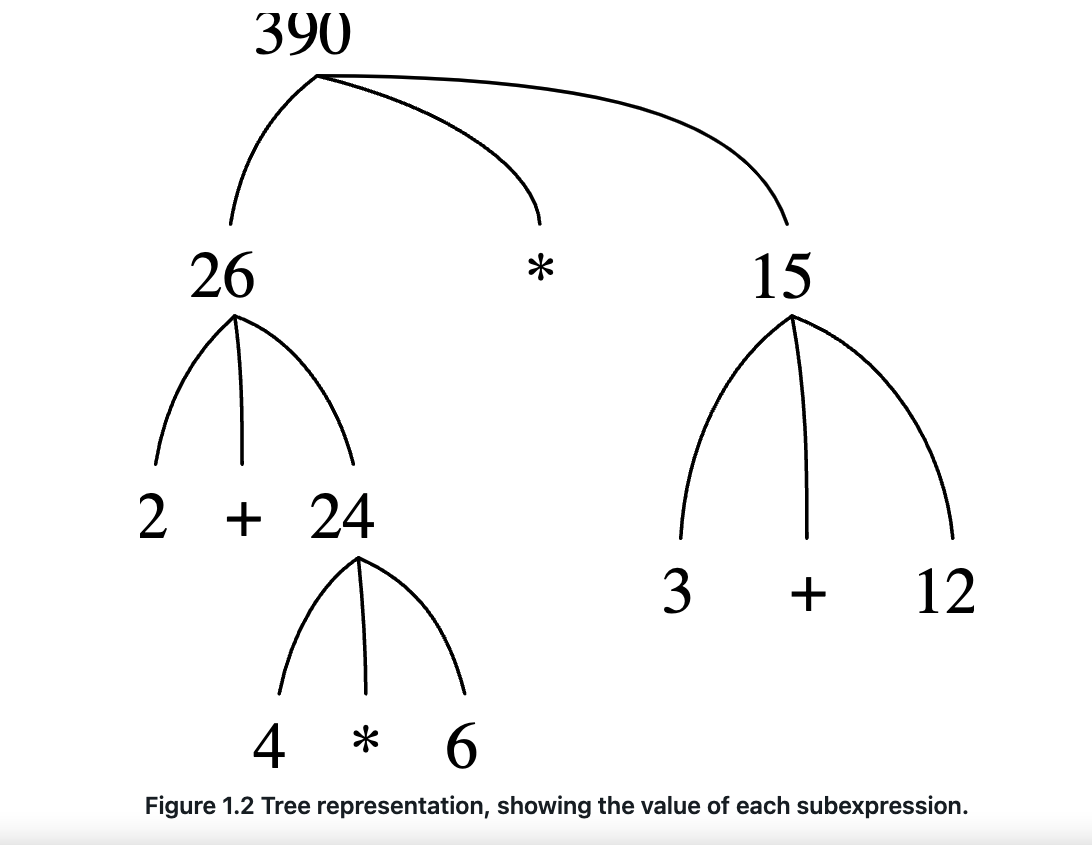
1.1.4 Compound Functions
Vocabulary
- compound functions: basically is an mean of combination(compound several expression) and mean of abstraction(as an unit, in most case this unit repesent an operate) of operate(compare to naming data, it abstract the data)
Questions
Notes
1.1.5 The Substitution Model for Function Application
Vocabulary
- substitution model: To apply a compound function to arguments, evaluate the return expression of the function with each parameter replaced by the corresponding argument.
- normal-order evaluation: fully expand and then reduce, js use substitution model because of effecy, but normal-order evaluation can be an extremely valuable tool
Questions
Notes
1.1.6 Conditional Expressions and Predicates
Vocabulary
- predicate: expression return true or flase
- expression__1&&_expression__2: expression__1?expression__2:false
- expression__1 || _expression__2: expression__1?true:_expression__2
- !expression: expression__1?false:true
Questions
Notes
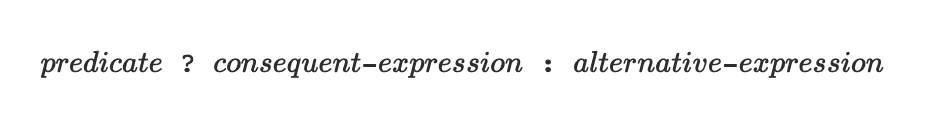
- Notice that && and || are syntactic forms, not operators; their right-hand expression is not always evaluated.
1.1.7 Example: Square Roots by Newton’s Method
Vocabulary
Questions
Notes
break a big program into several small pieces and construct them sperate
by using call function we can make a interative structure without any loop syntax
 see applicative order
see applicative order
it is crucial that each function accomplishes an** identifiable task** that can** be used as a module** in defining other functions. (how to finish the biggest task? break to into pieces, how to finish the pieces?…)
1.1.8 Functions as Black-Box Abstractions
Vocabulary
- black box: don’t care about** how to**, but** what is. **So a function should be able to suppress detail(hide the unnecessary details as far as possible)
- local name: the function param is not a matter, is used by the function’s author, must not affect them
- block structure: as a module, we declare all of the vars and functions inside a block structure {}, which make the boundary more clear(lexical scoping) encapsulation
Questions
Notes
- when read source code, first threat them as a black box, only care about what they done(their name), it can save your life
- We will use block structure extensively to help us break up large programs into tractable pieces.
1.2 Functions and the Processes They Generate
Vocabulary
Questions
- How to abstract functions?(how to split task?)
- How to predict the consequences of making a move?
Notes
- visualize the consequences
- A function is a pattern for the local evolution of a computational process. It specifies how each stage of the process is built upon the previous stage.
1.2.1 Linear Recursion and Iteration
Vocabulary
Linear Recursion(shape): a chain of defered operations, the interpreter keeps track of the operations to perform later on. the chain has n length. time O(n) storeO(n)
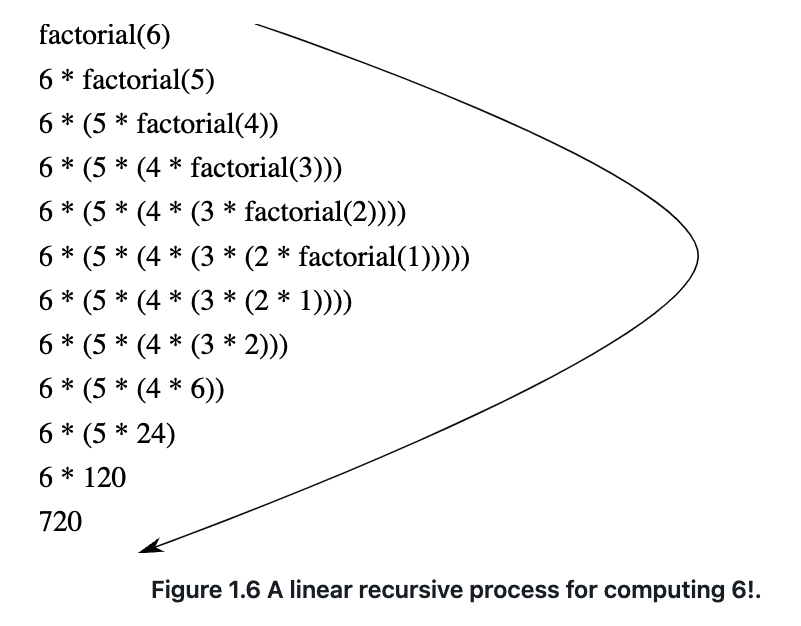
linear iterative: no need to grow and shrink. state can be summarized by a fixed number of state variables, together with a fixed rule that describes how the state variables should be updated as the process moves from state to state and an (optional) end test that specifies conditions under which the process should terminate.time O(n) store O(1)
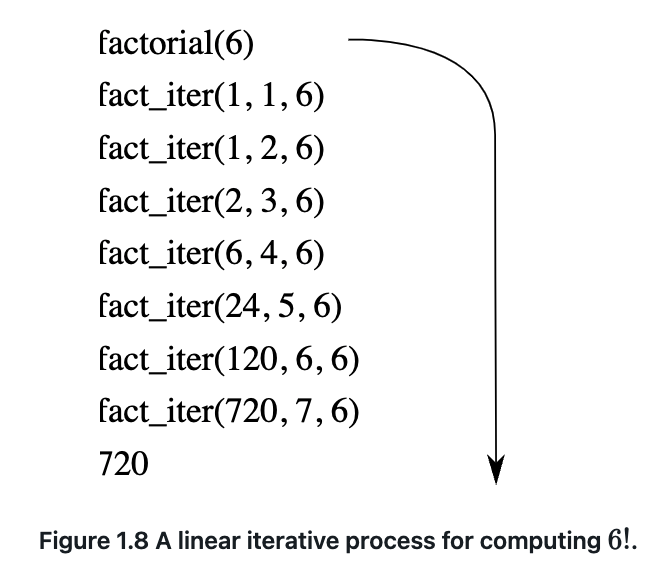
the difference: iterative process no need the interpreter to store some “hidden” state, all description are provided with state. And the recrusive process store state with the help of interpreter, the longer the chain is, the more state the interpreter should maintain.
recursive function: means a function syxnaxly refer itself, it has nothing to do with recursive process. a recursive function can be iterative process as well.
recursive process: it s a way of function evolves, leave the state to interpreter, and call the next function.
tail-recrusive: common language consume space even in iterative process’ recursive function. But js has tail-recrusive optimization, it consume constant space. With a tail-recursive implementation, iteration can be expressed using the ordinary function call mechanism, so that special iteration constructs are useful only as syntactic sugar.
Questions
Notes
- why recursive expand? I think it’s because we look problem from top to bottom, so we need to store “how to solve topest problem” all the time, and if you look problem from bottom to top, you only need to update the state and never need to care about the bottom problem solution(we aim at the topest problem)
1.2.2 Tree Recursion
Vocabulary
Questions
Notes
function call itself twice, it will form a binary-tree. we can anaysls O using tree graph.(it’s all about how to evolue function upon some ohter functions.)
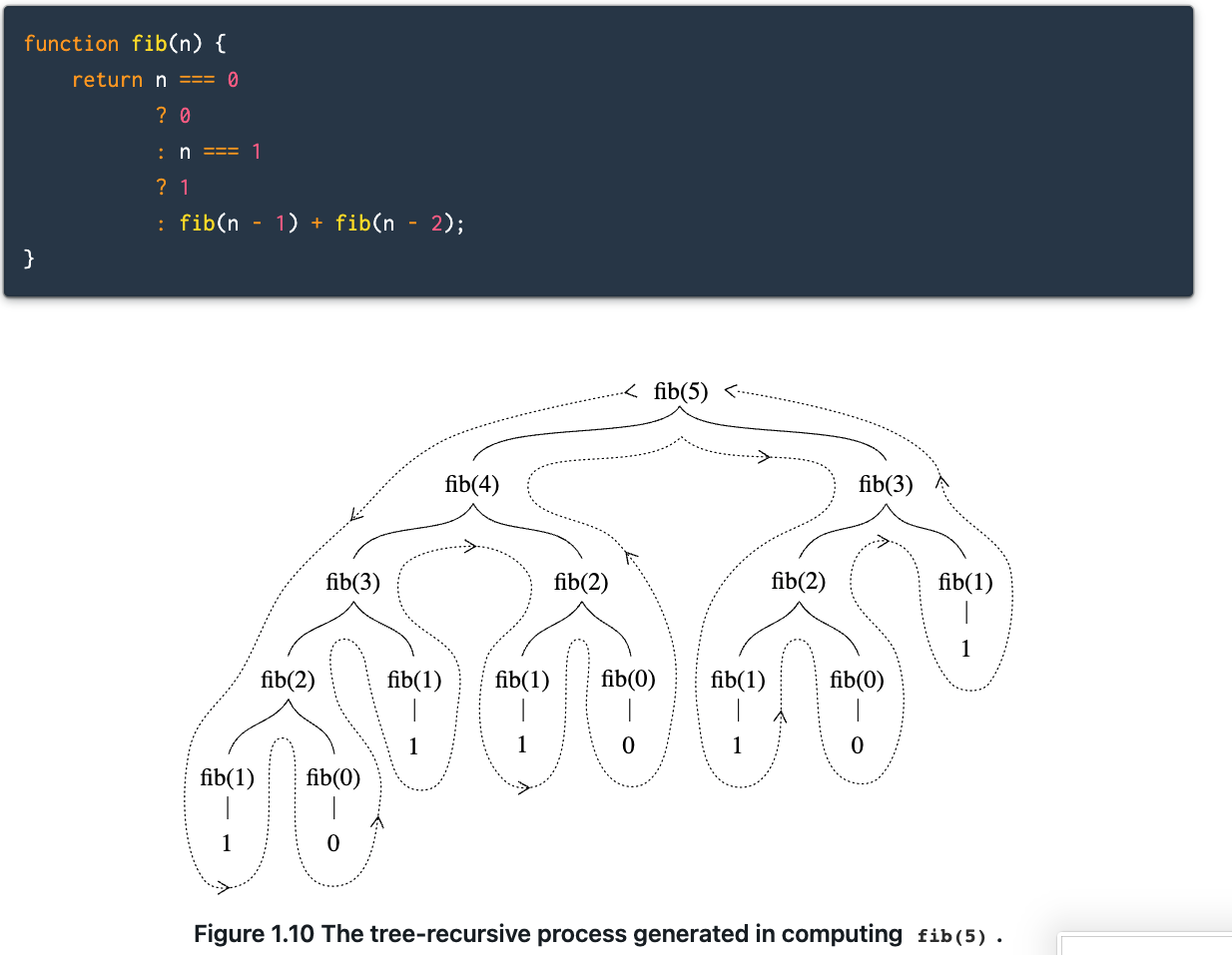
tree recursion is useful in tree structure data or graph, and more straightforward than interative process
change to interative process: thinking buttom to top, f(n) = f(n-1)+f(n-2), so f(n) + f(n-1) = f(n+1), we need two state to store n, n-1, and a limit condition count
1
2
3
4
5
6
7
8function fib(n){
function fib_iter(a, b, count){
return count === 0
? b
: fib_iter(a + b, a, count - 1);
};
return fib_iter(1, 0, n);
}Counting change
How many different ways can we make change of $1.00 (100 cents), given half-dollars, quarters, dimes, nickels, and pennies (50 cents, 25 cents, 10 cents, 5 cents, and 1 cent, respectively)?
1 | // problem: given 100 or n, count the ways of splitting it in |
Exercise 1.11
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15// recursive
function f(n) {
return n < 3
? n
: f(n - 1) + 2 * f(n - 2) + 3 * f(n - 3)
}
// iterative
function c_f(n) {
function f_iter(f1, f2, f3, count) {
return count === n
? f3
: f_iter(f1 + 2 * f2 + 3 * f3, f1, f2, count + 1)
}
return f_iter(2, 1, 0, 0)
}Exercise 1.12
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31// consider p[i][j]
// recursive
function p_recursive(i, j) {
return i === 1
? 1
: j === 1
? 1
: p_recursive(i - 1, j) + p_recursive(i, j - 1)
}
// iterative (dp)
function p(i, j) {
if(i < 1 || j < 1) throw new Error('number invalid')
if(i === 1 || j === 1) return 1
// create i + 1 row * j + 1 col array, init value = 0
const dp = new Array(i + 1).fill().map(item => new Array(j + 1).fill(0))
for(let k = 0; k < i + 1; k++) {
dp[k][1] = 1
}
for(let k = 0; k < j + 1; k++) {
dp[1][k] = 1
}
for(let k = 2; k < i + 1; k++) {
for(let g = 2; g < j + 1; g++) {
dp[k][g] = dp[k - 1][g] + dp[k][g - 1]
}
}
return dp[i][j]
}
// the author's solution use row, index to repesent the item, it's the same as mine
1.2.3 Orders of Growth
Vocabulary
- order of growth: a way to describe the computer resource that the process use. usually time and storage
- n: we describe a problem’s size as n.
- R(n): the resource used by n size problem.
Questions
Notes
1.2.4 Exponentiation
Vocabulary
Questions
Notes
- Exercise 1.16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64// fast expt: given b and n, calculate b^n
// naive: b^n = b * b * ..... * b (n time) or = b * b^n-1
// recursive time o(n) store o(n)
function expt(b, n) {
return n === 1
? b
: b * expt(b, n - 1)
}
// iterative store o(1)
function expt(b, n) {
function expt_iter(a, count) {
return count === n
? a
: expt_iter(a * b, count + 1)
}
return expt_iter(b, 1)
}
// mid: fast_expt: every step is the same, we can take a bigger step,
// b^n = (b^n/2)^2 n is even
// b^n = b * b^n-1 n is odd
// O(log n) store O(log n)
function is_even(n) {
return n % 2 === 0
}
function fast_expt(b, n) {
return n === 1
? b
: is_even(n)
? fast_expt(fast_expt(b, n / 2), 2) // wrong! use fast_expt(b, n / 2) * fast_expt(b, n / 2) instead this will overflow bcz (b, 2)
// still need to call fast_expt to solve
: b * fast_expt(b, n - 1)
}
// iterative
function fast_expt(b, n) {
function fast_expt_iter(a, count) {
return count === n // can use n to 0 method too
? a
: count * 2 <= n
? fast_expt_iter(a * a, count * 2)
: fast_expt_iter(a * b, count + 1)
}
return fast_expt_iter(b, 1)
}
// use bit shift, avoid use / instead use >> will be even more faster
function fast_expt(b, n) {
if(n === 0) return 1
let a = 1
while(n) {
if(n % 2 === 0) {
// b^n = (b^2)^n/2
n = n >> 1
} else {
n = n >> 1
a = a * b
}
b = b * b
}
return a
}
// 5 101
1.2.5 Greatest Common Divisors
Vocabulary
- GCD
Questions
Notes
辗转相除法:个人理解, 把a和b看成m份x和n份x,其中x为GCD(a, b),因为是最大公约数所以显然可以把a和b分成m/n份。a % b = r, = m * x - r * n * x = g * x, 他们的最大公约数仍然是x
1
2
3
4
5
6
7
8
9// GCD(a, b) = GCD(a, r) r = a % b
function gcd(a, b) {
return b === 0
? a
: gcd(b, a % b)
}
// 这个函数本身就是迭代的,从上往下不代表一定就是递归,只是思考的方式而已。更像与dp的区别
// 在其他语言,这个就是递归的,可以用for循环写迭代的。在js,有tail_recursive尾递归,这个就是
// for循环的语法糖 空间O(1)see the different process generated by normal order evaluation and applicate order evaluation
1.2.6 Example: Testing for Primality
Vocabulary
- divisors test: testing if there is divisors 1 < d < n. notes: n/d * d = n, so n/d or d one must less then sqrt(n) another one must bigger, if can’t find less then sqrt(n), then it’s clear that there will no more divisors bigger then sqrt(n).
- Fermat’s Little Theorem: If n is a prime number and a is any positive integer less than n, then a raised to the nth power is congruent to a modulo n.
- probabilistic algorithms: The existence of tests for which one can prove that the chance of error becomes arbitrarily small
Questions
Notes
divisors test
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39function is_prime(n) {
function divisor(a, b) {
return a % b === 0
}
function square(a) {
return a * a
}
function divisor_test(r, n) {
return square(r) > n
? true
: divisor(n, r)
? false
: divisor_test(r + 1, n)
}
return divisor_test(2, n)
}
// Exercise 1.23
// improve: if n can't be divided by 2, then all the even number can divide too
function *divisor_generator() {
let i = 2
yield i
i += 1
while(1) {
yield i
i = i + 2
}
}
/*
divisor.next()
{value: 2, done: false}
divisor.next()
{value: 3, done: false}
divisor.next()
{value: 5, done: false}
divisor.next()
{value: 7, done: false}
divisor.next()
{value: 9, done: false}
*/The fermat test
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30// if n is prime, then a^n mod n = a mod n, if 0 < a < n. O(time*logn)
function is_prime(n) {
function is_even(a) {
return a % 2 === 0
}
function square(a) {
return a * a
}
function random_int_less_than(a) {
return Math.floor(Math.random() * (a - 1)) + 1
}
function fast_expt_mod(a, n, m) {
return n === 0
? 1
: is_even(n)
? square(fast_expt_mod(a, n / 2, m)) % m // js uses 64bit represent number, take remainder each step for perventing overflow
: (a * fast_expt_mod(a, n - 1, m)) % m
}
function fermat_test(a, n) {
return fast_expt_mod (a, n, n) === a % n
}
function fermat_test_time(a, n, time) {
return time === 0
? true
: fermat_test(a, n)
? fermat_test_time(random_int_less_than(n), n, time - 1)
: false
}
return fermat_test_time(random_int_less_than(n), n, 10)
}
1 | // for testing the time cost of the function, we make a high order function |
1.3 Formulating Abstractions with Higher-Order Functions
Vocabulary
- function(review): function is a abstraction of some combinations of operation, for better reuse.
- high-order function: we need a way to abstract the operations to functions, that is, high-order function, pass function as parameter and return function as value.
Questions
Notes
- Often the same programming pattern will be used with a number of different functions.
1.3.1 Functions as Arguments
Vocabulary
Questions
Notes
- fn as args: consider the common partern of several functions, extract it as a high-order function.
- summation:
consider those three functions below:
1 | function sum_integers(a, b) { |
We can extract most of the part as a new function, and leave the difference as specify functions ‘term’ and ‘next’:
This is the summation in math: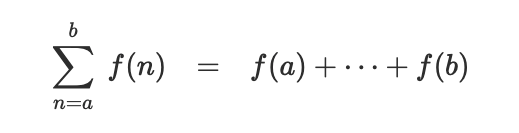
Exercise 1.29
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34function summate(a, b, f, next) {
return a > b
? 0
: f(a) + summate(next(a), b, f, next)
}
function simpson_integrate(a, b, f, n) {
const h = (b - a) / n
function get_y(k) {
return f(a + k * h)
}
function next(a) {
return a + 1
}
function is_even(a) {
return a % 2 === 0
}
function term(p) {
return p === 0
? get_y(p)
: p === n
? get_y(p)
: is_even(p)
? 2 * get_y(p)
: 4 * get_y(p)
}
return h / 3 * summate(0, n, term, next)
}
// iterative
function summate(a, b, f, next, res) {
return a > b
? res
: summate(next(a), b, f, res + f(a))
}Exercise 1.31
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42function product(a, b, f, next) {
return a > b
? 1
: f(a) * product(next(a), b, f, next)
}
function factorial(n) {
function inc(a) {
return a + 1
}
return product(1, n, a => a, inc)
}
function pi(n) {
function is_even(a) {
return a % 2 === 0
}
let i = 0
function numerator_next(a) {
i += 1
console.log(i)
return is_even(i)
? a
: 2 + a
}
let j = 0
function denominator_next(a) {
j += 1
return is_even(j)
? 2 + a
: a
}
return 4 * product(2, n, a => a, numerator_next)
/ product(3, n, a => a, denominator_next)
}
// iterative
function product(a, b, f, next) {
function product_iter(a, res){
return a > b
? res
: product_iter(next(a), res * f(a))
}
return product_iter(a, 1)
}Exercise 1.32
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32// use same thought to extract common partern of summate and product function
function summate(a, b, f, next) {
return a > b
? 0
: f(a) + summate(next(a), b, f, next)
}
function product(a, b, f, next) {
return a > b
? 1
: f(a) * product(next(a), b, f, next)
}
// what's the difference? what's the commons?
function accumulate(a, b, f, next, combine, null_value) {
return a > b
? null_value
: combine(f(a),accumulate(next(a), b, f, next, combine, null_value))
}
// 函数就是一个操作的抽象,普通函数可以抽象某个对data的操作,
// 而高阶函数把函数当作参数传入,则可以抽象某个对操作的操作,把某些操作的
// 相同部分抽离出来复用,也就是在两个ideas中找共同点
// 抽象的部分是相同的,而根据传来的参数的不同做特别的操作和结果
// iterative
function accumulate(a, b, f, next, combine, null_value) {
function accumulate_iter(a, res) {
return a > b
? res
: accumulate_iter(next(a),combine(res,f(a)))
}
return accumulate_iter(a, null_value)
}
1.3.2 Constructing Functions using Lambda Expressions
Vocabulary
- Lambda Expressions: Form like x => x + 4 without name. It’s convenient to pass to function as paramater. We use it when there’re some small expressions that uneccessary to declaire a function, particularly some functions that will never been reused.
- conditional statement(if else): make the expression to block, you can write more information in the block.
Questions
Notes
1.3.3 Functions as General Methods
Vocabulary
Questions
Notes
- Finding roots of equations by the half-interval method
given f(x), find the root of f(x) = 0. also given boundary a,b where root is between [a,b].
solution:
- naive way: enum a from b, to see if f(x) = 0 or close to 0. since a and b is continuous, the O depentend on the precision.
- half-interval: f(a) * f(b) < 0, if and only if root is between a, b. we take the middle of a, b x to validate if f(x) * f(a) or f(x) * f(b) < 0. set x as a or b again and narrow the range. End when the range is small than T. O(log(b-a)/T). We can see T as the smallest unit, as if T equal 1 then O(log(b-a)).
1 | function find_root(f, r, a, b) { |
1.3.4 Functions as Returned Values
Vocabulary
Questions
Notes
- fn as paramater: mean of abstraction the compose / operate function
- fn as return value: make a new function base on original function, usually warp some extra logic to the function, or compose several function to one.
1 | // example 1: make a damp to a function for instance x -> x * x |
This is a strengthen of expression, without fn as param we can not express abstraction of operation that operate other function. without fn as return value we can not express the abstraction of warping / upgrade a function use extra logic.
- derivative: Dg(x)=(g(x+dx)−g(x))/dx, dx as a small number, we calculate the difference of g(x) between x + dx and x, then divide with dx.
1 | // deriv is a new function base on g(x), so we can use fn as return value to |
- We began section 1.3 with the observation that compound functions are a crucial abstraction mechanism, because they permit us to express general methods of computing as explicit elements in our programming language. Now we’ve seen how higher-order functions permit us to manipulate these general methods to create further abstractions.
- we should always be alert to opportunities to identify the underlying abstractions in our programs and create more powerful abstractions, but that doesn’t mean one should always write programs in the most abstract way possible. expert programmers know how to choose the level of abstraction appropriate to their task. But it is important to be able to think in terms of these abstractions, so that we can be ready to apply them in new contexts.
- first-class elements: programming languages impose fewest restriction of manipulate them.
- They may be referred to using names.
- They may be passed as arguments to functions.
- They may be returned as the results of functions.
- They may be included in data structures.
- js fn as first-class elements: more experssive, but the efficient implemant is a challenge.
- Exercise 1.40
1 | // given param, generate a function |
- Exercise 1.41
1 | function double(f) { |
- Exercise 1.42
1 | // abstraction of compose |
- Exercise 1.43
1 | // given a function and n times, modify the function to repeat itself n times |
- Exercise 1.44
1 | // smoothing function, times |
- Exercise 1.46
iterative improvement: in order to compute result, we first start at a initial guess, then judge whether it is good enough, if no, repeat the process.
1 | function iterative_improve(improve, is_good_enough) { |
- abstractions we have for now:
- naming: abstraction of express
- function: abstraction of operate
- basic function: abstraction of operate data
- high-order function:
- function as param: abstraction of operate function(compose funtion)(idea)
- function as return value: abstraction of modify / update function(idea)
It is all about increasing your ability of expression.
sicpjs — Apr 25, 2022
Made with ❤ and at Earth.

