SICPJS 2. Building Abstractions With Data

(Updated: )

Vocabulary

Questions

Notes

  • Compound data: just like compound function, we enhance our expressive power of our language. And elevate the conceptual level at which we can design our programs.
  • Glue data together: compound data glue data together to reduce the complexity of system.
  • Data abstraction: modularity data can separate the part of function to deal with data and the part to deal with how the data be repesented.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
// repesent, and deal with rational number
// if don't have compound data

const a_numerator = 1
const a_denominator = 4

const b_numerator = 1
const b_denominator = 5

// there's no way you can handle these two rational number without care
// about how they be repesented.

// compound data

const a = {
  numerator: 1,
  denominator: 4
}

const b = {
  numerator: 1,
  denominator: 5
}

function add(a, b){
  return {
    numerator: a.numerator + b.numerator,
    denominator: a.denominator + b.denominator
  }
}

function add_and_multi(a, b){
  return multi(a, add(a, b))
}

// we don't need to care about how a, b repesent data,
// we just abstract how add() and multi() process a, b

2.1 Introduction to Data Abstraction

Vocabulary

  • Data abstraction: compare to function abstraction, data abstraction hide the detail of how to compound it and expose what is

Questions

Notes

  • The basic idea of data abstraction is to structure the programs that are to use compound data objects so that they operate on “abstract data.” That is, our programs should use data in such a way as to make no assumptions about the data that are not strictly necessary for performing the task at hand.

2.1.1 Example: Arithmetic Operations for Rational Numbers

Vocabulary

Questions

Notes

  • Wishful thinking: assuming something that we have even we not yet implement them, then build something upon them.
  • The step of abstract the arithmetic operations of rational:
    • We operate base on data abstraction, so we first hide the detail of data abstraction(wishful thinking)
    • We assume that we can construct a rational number, and can extracting its numerator and denominator.
1
2
3
function make_rati(n, d) // make rational number which equal n / d
function numer(r) // extract rational number's numerator
function denom(r) // extract rational number's denominator
1
2
3
4
function add(a, b) {
  return make_rati((numer(a) * denom(b) + numer(b) * denom(a)) / denom(a) * denom(b))
}
// ...
  • use pair to implement the assuming functions make_rati, numer, denom.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
function pair(head, tail) // construct a pair with head and tail
function head(pair) // return pair's head
function tail(pair) // return pair's tail

function make_rati(n, d) {
  const m = gcd(n, d)
  return pair(n / m, d / m)
}

function numer(rati) {
  return head(rati)
}

function denom(rati) {
  return tail(rati)
}
  • Exercise 2.1
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    // handle positive and negative, we only change make_rati
    // since it is the only function that modify/create pair
    function make_rati(n, d) {
      const m = gcd(n, d)
      if(n * d > 0) {
        return pair(n / m, d / m)
      } else if(n * d < 0) {
        if(n < 0) {
          return pair(n / m, d / m)
        } else {
          return pair(n / m, -d / m)
        }
      }
      // 'd is zero needs handle'
    }

    // if don't use * to judge, can make some helper function
    function make_rati(n, d) {
      const m = gcd(n, d)
      // abstract n and d, only use the sign to compute
      // think about is it necessary to use n and d directly
      // or we can extract the essence to compute
      function sign(x) {
        return x < 0
               ? -1
               : x > 0
               ? 1
               : 0
      }
      function abs(x) {
         return x < 0
                ? -x
                : x;
      }
      return pair(sign(n) * sign(d) * abs(n / m), abs(d / m))
    }

2.1.2 Abstraction Barriers

Vocabulary

Questions

Notes

  • In general, the underlying idea of data abstraction is to identify for each type of data object a basic set of operations in terms of which all manipulations of data objects of that type will be expressed, and then to use only those operations in manipulating the data.

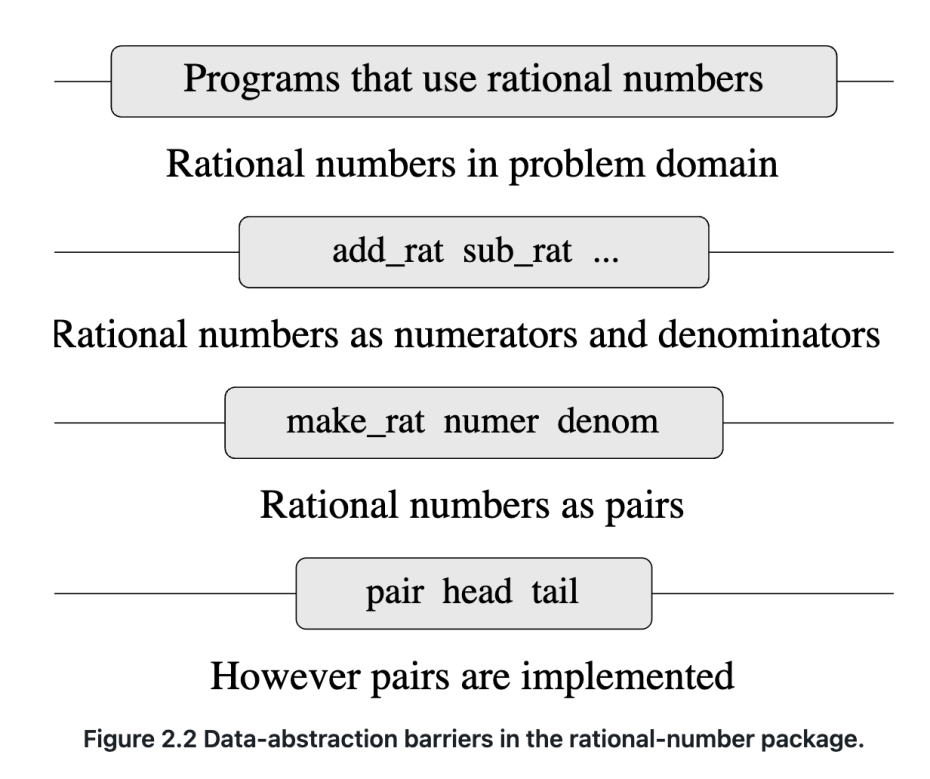    Abstraction Barriers The horizontal lines represent _abstraction barriers_ that isolate different "levels" of the system. The barriers will hide the implement details below it. All complex data can be repesent by some ways using primitive data. How to repesent data influnences the programs that operate it. But if we only modify the implementation that will not affect the programs build upon it. The data-abstraction methodology gives us a way to defer that decision without losing the ability to make progress on the rest of the system. (For example, fe no need to wait until the be api finished, fe can start develop whenever the api document(interface) is given).

  • Exercise 2.2

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
// from top to bottom, using data-abstraction barriers to construct the system
// for calculate midpoint of segment, we need make_segment
// and extract start_segment and end_segement
// use interface to abstract
interface segment {
  make_segment: (start, end) => segment
  start_segment: (segment) => point
  end_segment: (segment) => point
}
function midpoint_segment(segment) {
  return avg_point(start_segment, end_segment)
}

function make_segment(start, end) {
  return pair(start, end)
}
function start_segment(segment) {
  return head(segment)
}
function end_segment(segment) {
  return tail(segment)
}

interface point {
  make_point: (x, y) => point
  x_point: (point) => a
  y_point: (point) => b
  avg_point: (start, end) => point
}

function make_point(x, y) {
  return pair(x, y)
}
function x_point(point) {
  return head(point)
}
function y_point(point) {
  return tail(point)
}
// avg use point abstraction
function avg_point(start, end) {
  return make_point((x_point(start) + x_point(end)) / 2, (y_point(start) + y_point(end)) / 2)
}
  • Exercise 2.3
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
interface {
  distence_segment: (a, b) => distence
}

function make_rectange(a, b, c, d) {
  const a_b = pair(a, b)
  const c_d = pair(c, d)
  return pair(a_b, c_d)
}
function a_rectange(r) {
  return head(head(r))
}
// ...
function get_w_and_h(r) {
  const a_to_b = distence_segment(a_rectange(r), b_rectange(r))
  const a_to_c = distence_segment(a_rectange(r), c_rectange(r))
  return pair(a_to_b,a_to_c)
}
function perimeter(r) {
  const w_h = get_w_and_h(r)
  return (head(w_h) + head(w_h)) * 2
}
function area(r) {
 const w_h = get_w_and_h(r)
  return head(w_h) * head(w_h)
}
function get_w_and_h(r) {
  const a_to_b = distence_segment(a_rectange(r), b_rectange(r))
  const a_to_c = distence_segment(a_rectange(r), c_rectange(r))
  return pair(a_to_b,a_to_c)
}

2.1.3 What Is Meant by Data?

Vocabulary

  • Data: as defined by some collection of selectors and constructors, together with specified conditions that these functions must fulfill in order to be a valid representation.

Questions

Notes

  • If one can obey the rules and implement the selectors and onstructors, it can use as the data. It should not matter how it implement.
  • Message passing: use function represent data, and pass a message to get specify return.
  • message passing pair
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
// fulfill: z = pair(x, y) head(z) = x tail(z) = y
function pair(x, y) {
  function dispatch(m) {
    return m === 0
           ? x
           : y
  }
  return dispatch
}
function head(z) {
  return z(0)
}
function tail(z) {
  return z(1)
}

// 只要满足规则就可以代表数据，背后是不是真的是一个存储的变量已经不重要了，pair(x, z) 返回（生成）
// 了一个规则可以返回x和y
  • Exercise 2.4
1
2
3
function tail(z) {
  return z((x, y) => y)
}
  • Exercise 2.5
1
2
3
4
5
6
7
8
9
10
11
12
13
function pair(a, b) {
  return fast_expt(2, a) + fast_expt(3, b)
}
function head(p) {
  return p % 2 === 0
         ? head(p / 2) + 1
         : 0
}
function tail(p) {
  return p % 3 === 0
         ? tail(p / 3) + 1
         : 0
}
  • Exercise 2.6
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
const zero = f => x => x

function add_1(n) {
  return f => x => f(n(f)(x))
}

// add_1(zero)

const one = f => x => f(x)

const two = f => x => f(f(x))

function plus(p, q) {
  return f => x => (p(f)(q(f)(x)))
}

2.1.4 Extended Exercise: Interval Arithmetic

Vocabulary

Questions

Notes

  • Exercise 2.7
1
2
3
4
5
6
7
8
9
function make_interval(x, y) {
  return pair(x, y)
}
function upper_bound(i) {
  return tail(i)
}
function lower_bound(i) {
  return head(i)
}
  • Exercise 2.8
1
2
3
function sub_interval(x, y) {
  return add_interval(x, make_interval(lower_bound(y),upper_bound(y)))
}
  • Exercise 2.9
1
2
3
4
5
6
7
// proof: width A + width B = width C, where C is A + B (interval)
// A + B = C => upper(A) + upper(B) = upper(C), lower(A) + lower(B) = lower(C)
// width A + width B  = (upper(A) - lower(A)) / 2 + (upper(B) - lower(B)) / 2 
// = (upper(A) + upper(B) - (lower(A) + lower(B))) / 2 = (upper(C) - lower(C)) / 2 
// = C

[1, 2] * [1, 2] = [1, 4]
  • Exercise 2.10
1
2
3
4
5
function div_interval(x, y) {
  return lower_bound(y) <= 0 && upper_bound(y) >= 0
         ? signal('x can't be zero')
         : mul_interval(x, make_interval(lower(y),upper(y)))
}
  • Exercise 2.11
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
function mul_interval(x, y) {
  if(lower_bound(x) <= 0 && lower_bound(y) <= 0) {
    if(upper_bound(x) >= 0 && upper_bound(y) >= 0) {
      const p1 = upper_bound(x) * upper_bound(y)
      const p2 = lower_bound(x) * lower_bound(y)
      const p3 = upper_bound(x) * lower_bound(y)
      const p4 = upper_bound(y) * lower_bound(x)
      return make_interval(math_min(p1, p2, p3, p4),
                         math_max(p1, p2, p3, p4))
    }
    return make_interval(upper_bound(x) * upper_bound(y),
                         lower_bound(x) * lower_bound(y))
  } else {
    return make_interval(lower_bound(x) * lower_bound(y),
                         upper_bound(x) * upper_bound(y))
  }
}
  • Exercise 2.12
1
2
3
4
5
6
7
8
9
function make_center_percent(c, p) {
  return make_interval(c * (1 - p), c * (1 + p))
}
function center(i) {
  return (lower_bound(i) + upper_bound(i)) / 2
}
function percent(i) {
  return ((upper_bound(i) - lower_bound(i)) / 2) / center(i)
}
  • Exercise 2.13
1
2
3
4
// a * b -> pa * pb
function mul_interval(x, y) {
  return make_center_percent(center(x) * center(y), percent(x) * percent(y))
}

If we only see two endpoints, some problems will become harder to solve. But if we change aspect to see data, it will be come eaiser.